Les inégalités monétaires concernent le patrimoine et les revenus
Lorsqu’il est question d’inégalités monétaires, le plus courant est d’étudier les inégalités de patrimoine et de revenus. Ces deux concepts doivent être clairement définis.
1.1. Définir et mesurer les inégalités de patrimoine
Selon l’Insee, le patrimoine des ménages noteinegalites2 inclut le patrimoine financier (actifs financiers, épargne…), immobilier et les biens professionnels (importants notamment pour les agriculteurs et les praticiens libéraux qui accumulent des biens indispensables à leur activité professionnelle).
On distingue ensuite le patrimoine brut du patrimoine net. Le patrimoine net correspond au patrimoine brut duquel est déduit le montant du capital dû dans le cas d’emprunts contractés.
Pour l’évaluer, l’Insee réalise aujourd’hui des enquêtes panélisées (i.e. en interrogeant périodiquement un même groupe de ménages sur son patrimoine). Pour remonter plus loin dans le temps, il est possible d’estimer le patrimoine de ménages à partir de la fiscalité successorale (i.e. les déclarations de succession) des ménages. En effet, la fiscalité successorale a été mise en place avant la fiscalité des revenus. noteinegalites3
Toutefois, même si la notion de patrimoine peut sembler idéale pour mesurer la richesse d’un ménage, elle ne prend pas en compte les gains futurs de certains investissement présents – c’est notamment le cas des investissements dans l’éducation qui, en général, se traduisent par des salaires futurs plus importants et donc un patrimoine futur plus important. noteinegalites4
Pour étudier les inégalités de patrimoine, on fait appel à deux notions statistiques : la distribution et les déciles (voir encadré ci-dessous).
Comprendre les notions de distribution et décile
Quand on s’intéresse aux inégalités de patrimoine, on étudie la distribution du patrimoine, c’est-à-dire la manière dont se répartissent les patrimoines en France.
Les statisticiens cherchent ensuite à classer la population (ou les ménages) par ordre croissant de patrimoine, du plus faible au plus élevé. Pour cela, ils découpent, le plus souvent, la population en 10 groupes de taille égale : cela signifie que l’on scinde la population, selon son patrimoine, par tranche de 10%.
Concrètement, les 10% de la population avec le patrimoine le plus faible sont dans le premier groupe, les 10% suivants dans le deuxième groupe… et enfin les 10% avec le patrimoine le plus élevé sont dans le dixième groupe.
La valeur qui sépare le 1er groupe du second est nommée premier décile (D1) : en d’autres termes, le premier décile est le montant du patrimoine au-dessous duquel se trouvent les 10% de patrimoines les plus faibles et au-dessus duquel se situent 90 % des patrimoines. La valeur qui sépare le second du troisième groupe est le second décile (D2), etc. et la valeur qui sépare le 9e groupe du 10e groupe est le neuvième décile (D9). Le neuvième décile est la valeur du patrimoine au-dessous duquel se situent 90% des patrimoines et au-dessus duquel se situent les 10% des patrimoines les plus élevés.
Les notions de distribution et de décile sont également utilisées pour étudier d’autres types d’inégalités comme les inégalités de revenus.
La répartition des patrimoines en France et les niveaux de patrimoine des plus riches et des plus pauvres peuvent être illustrés par le premier graphique ci-dessous.
Déciles de patrimoine brut et net en France en 2018 (en euros)
Lecture : en France, en 2021, 10% des ménages ont un patrimoine brut supérieur à 607 700€ et 40% des ménages ont un patrimoine brut inférieur à 100 000€.
1.2 L’évolution du patrimoine des grandes fortunes
Les débats récents sur les grandes fortunes et l’enrichissement des milliardaires invitent à s’intéresser à l’évolution de leurs patrimoines. A ce titre, une récente étude d’Oxfam révèle que durant la crise du COVID-19 les 10 hommes les plus riches au monde ont vu leur patrimoine doubler – ils possèdent aujourd’hui plus que ce que les 3,1 milliards de personnes les plus pauvres détiennent – tandis que 99% de l’humanité a eu des revenus moins importants que prévu durant cette même période.
Pour aller plus loin, observons l’évolution du patrimoine des quelques plus grandes fortunes du monde sur une plus longue période, en nous intéressant, dans un premier temps, au patrimoine des milliardaires. noteinegalites5 Le nombre de milliardaires a augmenté, passant de 140 en 1987 à plus de 1400 en 2013. Sans surprise, la somme de leurs patrimoines a également augmenté, multipliée par près de vingt durant cette période. noteinegalites6 Toutefois, sachant qu’il y a plus de personnes dans ce groupe, il n’y a rien d’étonnant à ce que la somme de leurs fortunes soit plus grande. Il n’est donc pas évident de mesurer leur enrichissement à partir de ces données.
Si on rapporte le nombre de milliardaires à la population mondiale et si on rapporte leur patrimoine à celui du patrimoine privé noteinegalites7 mondial, on voit qu’en 1987 il y avait 5 milliardaires pour 100 millions de personnes et qu’en 2013 il y en avait 30. En parallèle, le cercle des milliardaires détenait 0,4% du patrimoine privé mondial en 1987, contre 1,5% en 2013. noteinegalites8 Ce n’est donc pas non plus suffisant pour en déduire une évolution claire des inégalités de patrimoine : comme ce groupe représente une plus grande part de la population mondiale aujourd’hui qu’à la fin des années 1980, il n’y a rien de surprenant à ce que la part du patrimoine mondial détenu chaque année par l’ensemble des milliardaires ait augmenté.
Une manière de mieux comprendre la dynamique du patrimoine des grandes fortunes est d’étudier l’évolution de la part du patrimoine d’un pourcentage fixe de la population mondiale. Par exemple, on peut étudier le cas des 0,00000005% plus hauts patrimoines au monde (soit les 143 plus hauts patrimoines en 1987, et les 234 plus hauts patrimoines en 2013). Comme l’illustre la figure ci-dessous, on constate que ce groupe restreint, bien que représentant toujours la même part de la population mondiale, a vu la part de son patrimoine tripler entre 1987 et 2013, passant de 0,31% à 0,91% du patrimoine privé mondial.
Cette évolution témoigne ainsi d’une hausse substantielle des inégalités de patrimoine à l’échelle mondiale entre les quelques plus grandes fortunes et le reste du monde.
Part en % des 0,00000005% plus hauts patrimoines au monde dans le patrimoine privé mondial (1987-2013)
Lecture : en 1987, les 0,00000005% des plus hauts patrimoines mondiaux détenaient 0,31% du patrimoine privé mondial.
Source Thomas Piketty, Le capital au XXIe siècle, Seuil, 2013, p 694.
1.3 Définir et mesurer les inégalités de revenus
Les revenus offrent une autre approche possible pour mesurer les inégalités monétaires.
1.3.1 Ne pas confondre revenu et salaire
Le « salaire », que l’on désigne plutôt par revenu salarial, correspond à la somme des salaires perçus par un individu sur une année donnée, nets de toutes cotisations sociales. Le revenu salarial capte, dans une certaine mesure, la « richesse » d’un individu mais ne comptabilise pas les prestations sociales, les taxes ou encore les revenus du capital. Or, cette donnée est importante dans le cadre d’études sur les inégalités monétaires puisque taxes et prestations sociales sont des mécanismes de redistribution des richesses mis en place par l’État pour corriger certaines inégalités.
1.3.2 Définition de la notion de revenu disponible
Ainsi, pour étudier les inégalités de revenus, il paraît plus pertinent de tenir compte de ces mécanismes de redistribution. Pour cela, on va préférer la notion de revenu disponible à celle de revenu salarial pour étudier les inégalités de revenus.
« Le revenu disponible est le revenu à la disposition du ménage pour consommer et épargner. Il comprend les revenus d’activité nets des cotisations sociales, les indemnités de chômage, les retraites et pensions, les revenus du patrimoine (fonciers et financiers) et les autres prestations sociales perçues, nets des impôts directs. » (source : Insee)
Une des dernières études de l’Insee sur les questions de revenus et de patrimoine en France offre une représentation des revenus disponibles des ménages en France en 2018 (voir ci-dessous).
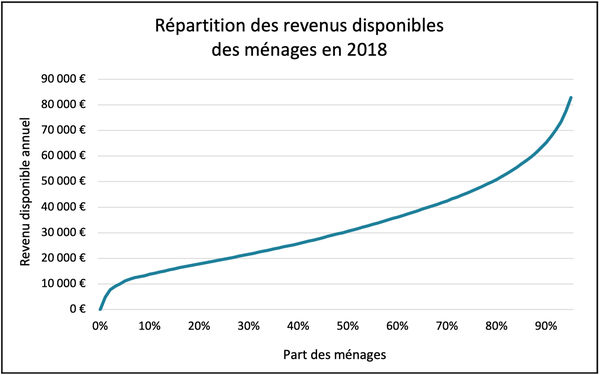
Répartition des revenus disponibles des ménages en 2018
Lecture : en 2018, 50 % des ménages ont un revenu disponible annuel inférieur à 30 620 euros.
Une limite importante de l’utilisation des revenus pour mesurer les inégalités reste la non prise en compte des dépenses pré-engagées (ou dépenses contraintes). Celles-ci se caractérisent par le fait qu’elles sont obligatoires en raison de la loi ou de la signature d’un contrat. Elles incluent notamment les loyers, le remboursement de prêts ou encore certaines factures (énergie, eau, abonnements aux services de télécommunications etc.). Ces dépenses pré-engagées peuvent cacher d’autres inégalités – notamment parce que leur part dans le budget d’un ménage diminue avec l’élévation du niveau de vie.
1.4 La taille des ménages : une donnée importante dans le calcul des inégalités de revenus
1.4.1 Pour évaluer le niveau de vie d’un ménage, la notion d’unité de consommation est préférable à celle de ménage
L’étude précédemment citée de l’Insee s’intéresse à la répartition des revenus et des patrimoines en France en comparant les ménages entre eux. Considérons deux ménages avec le même patrimoine et les mêmes revenus. Si le premier ménage est un couple sans enfants et le second est un couple avec 2 enfants, alors, intuitivement, le couple sans enfants est plus aisé (il vit « mieux ») que celui avec enfants. Cette intuition traduit le fait que la taille du ménage est une donnée importante lorsqu’il est question d’inégalités de revenus. Or, le revenu disponible d’un ménage est indépendant du nombre d’individus qui le constituent.
Pour répondre à cette problématique, on remplace parfois le revenu disponible par le niveau de vie. Le niveau de vie d’un ménage, exprimé en euros, correspond à son revenu disponible que l’on divise par un nombre qui dépend de la taille et du profil du ménage (plus il y a d’individus dans le ménage, plus ce nombre est grand). On appelle ce nombre le nombre d’unités de consommation (UC) du ménage.
1.4.2 Différentes méthodes permettent de calculer le nombre d’unité de consommation d’un ménage
Une méthode couramment utilisée, par l’Insee notamment, consiste à dire que l’on attribue 1 UC au premier adulte du ménage, 0,5 UC aux autres personnes de 14 ans ou plus et 0,3 UC aux enfants de moins de 14 ans. noteinegalites9 Cette méthode, dite « échelle d’équivalence de l’OCDE modifiée », n’est pas la seule manière de déterminer le nombre d’UC d’un ménage.
A ce titre, l’OCDE a récemment préféré une autre méthode, dite « échelle d’équivalence en racine de N ». Concrètement, le nombre d’UC du ménage ne dépend alors que du nombre d’individus dans le ménage, quels que soient les âges des individus le composant. noteinegalites10 Comme nous avons pu l’évoquer dans une autre fiche sur le calcul du PIB, le choix de la convention est un choix humain et chaque convention a ses biais, avantages et inconvénients.
Au-delà de considérations techniques, retenons ici que le niveau de vie, qui s’exprime en euros, permet de comparer les revenus de ménages de tailles différentes et que plusieurs conventions existent pour calculer le niveau de vie d’un ménage.
 Pour en savoir plus
Pour en savoir plus
Le coefficient de Gini, un indicateur synthétique d’inégalités de revenus
Le coefficient de Gini est un indicateur d’inégalités couramment utilisé. Il s’agit d’un indicateur dit « synthétique », c’est-à-dire qu’il résume en un chiffre unique la distribution des revenus, en pondérant et agrégeant l’ensemble des revenus (en savoir plus sur les indicateurs synthétiques dans notre module sur le PIB, la croissance et les limites planétaires).
2.1 Qu’est-ce que le coefficient de Gini ?
Le coefficient (ou indice) de Gini est un indicateur de distribution du revenu développé au début du 20e siècle. Sa valeur est comprise entre 0, qui correspond à une « égalité parfaite » (chaque ménage reçoit la même fraction des revenus) et 1, qui représente une « inégalité parfaite » (la fraction de la population la plus riche reçoit l’intégralité des revenus). La pertinence du coefficient de Gini vient du fait qu’il prend en compte l’ensemble de la distribution des revenus dans la population (indicateur « synthétique »).
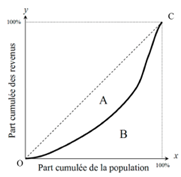
Pour l’obtenir, il faut passer par la courbe dite de Lorenz (en référence à l’économiste Max O. Lorenz). Elle représente, en ordonnée, la part du revenu détenue par la proportion, en abscisse, de la population (classée par revenus croissants, donc du plus pauvre au plus riche), comme l’illustre la figure ci-dessous.
La courbe de Lorenz joint toujours l’origine (point O) au point de coordonnées (100%, 100%) (point C) ce qui traduit le fait que si l’on considère toute la population, on englobe bien l’ensemble des revenus des ménages. Si la courbe de Lorenz est une droite (la droite qui lie O et C sur la figure), c’est que tous les ménages ont les mêmes revenus. A contrario, dans le cas extrême où une personne accaparerait tous les revenus d’un pays, la courbe serait en deux morceaux : une horizontale jusqu’à 100% puis une verticale jusqu’au point C.
Le coefficient de Gini est égal au rapport entre la surface A et la surface du triangle A+B (égale à ½). Il est compris entre 0 et 1 et est d’autant plus élevé que la distribution est inégalitaire.
2.2 Quelques exemples de l’emploi du coefficient de Gini
Le coefficient de Gini permet de comparer les inégalités entre pays. Nous représentons ci-dessous les coefficients de Gini pour le niveau de vie dans les pays de l’Union européenne en 2019. Ils sont classés par ordre croissant. Ainsi, la Slovaquie est le pays le plus égalitaire avec un coefficient de Gini de 0,209 tandis que la Bulgarie est le pays le plus inégalitaire, selon cette mesure, avec un coefficient de Gini de 0,400.
Coefficient de Gini pour les pays de l'Union européenne en 2019
Lecture : en 2019, en Slovaquie, le coefficient de Gini est de 0,209.
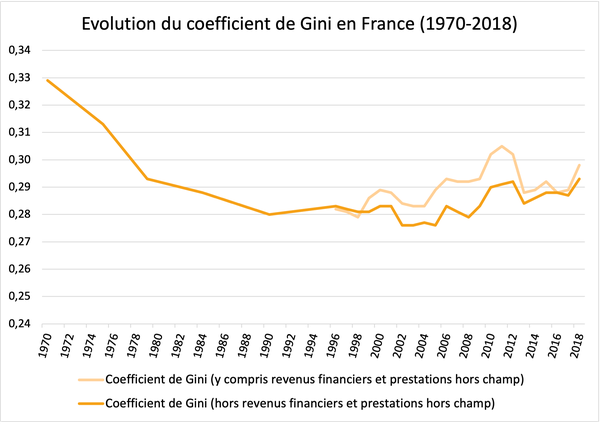
Il est également intéressant de visualiser l’évolution du coefficient de Gini pour un pays donné. Prenons le cas de la France où l’on représente ci-dessous l’évolution du coefficient de Gini entre 1970 et 2018. Cette représentation est d’autant plus pertinente que le débat public se limite parfois à une vision court-terme de l’évolution des inégalités tandis qu’une vision long-terme offre une perspective plus globale. Ainsi, en France le coefficient de Gini a d’abord baissé entre les années 1970 et 1990 (résorption des inégalités) avant de remonter dans les années 2000, avec un pic en 2011. Même si on peut aujourd’hui se réjouir d’une baisse des inégalités entre 2011 et 2017-18, il n’en reste pas moins que le niveau des inégalités de revenus aujourd’hui est supérieur à celui des années 1980-90.
Evolution du coefficient de Gini en France (1970-2018)
Source Insee,
Revenus et patrimoine des ménages, édition 2021.
Note : le niveau de vie correspond au revenu disponible du ménage rapporté au nombre d’unités de consommation (calculé selon la méthode de l’échelle de l’OCDE modifiée). Les prestations hors champs incluent notamment les allocations aux adultes handicapés.
Lecture : en 1970, le coefficient de Gini en France est de 0,329.
2.3 Les limites du coefficient de Gini
La pertinence du coefficient de Gini, qui repose sur le fait qu’il considère l’ensemble de la distribution des revenus, amène également à une critique. En effet, il ne permet pas de spécifier d’où viennent les inégalités. Cet indicateur peut donner l’illusion de résumer l’ensemble des inégalités en un seul chiffre alors que, au contraire, il apporte une vision « aseptisée » et difficile à décrypter des inégalités ne permettant pas de déterminer leurs caractéristiques. noteinegalites11
Des études noteinegalites12 ont ainsi montré que le coefficient de Gini est particulièrement sensible à des changements de revenus au milieu de la distribution (c'est-à-dire que l’indicateur est sensible à des changements qui concernent les ménages avec un revenu proche du revenu moyen en France). On peut alors argumenter que ce n’est pas nécessairement ce que l’on cherche à mettre en exergue quand on mesure des inégalités – on cherche davantage à étudier la répartition des revenus dans les tranches les plus riches et les plus pauvres.
2.4 D’autres indicateurs synthétiques : l’indicateur de Theil et l’indice d’Atkinson
A l’instar du coefficient de Gini, d’autres indicateurs synthétiques permettent une évaluation des inégalités de revenus. Parmi ceux-ci, nous pouvons citer l’indicateur de Theil et l’indice d’Atkinson.
L’indicateur de Theil est, comme le coefficient de Gini, d’autant plus élevé que l’on s’éloigne de l’égalité parfaite. De plus, plus les revenus sont dispersés dans la distribution, plus il est élevé. Son intérêt principal est de pouvoir être décomposé en différents sous-groupes dans la population et ensuite être additionné pour ces différents sous-groupes. noteinegalites13 Par exemple, considérons que l’on partitionne la population en 3 groupes ou classes (une classe aisée, une classe moyenne et une classe populaire). L’indice de Theil peut s’écrire comme une somme de deux termes :
- un terme qui mesure les inégalités au sein de chaque classe (inégalité intraclasse) : cela traduit par exemple qu’au sein des « riches », il y a des « très riches » et des « un peu moins riches » ;
- un terme qui évalue les inégalités entre les 3 classes (inégalité interclasse).
L’indice d’Atkinson traduit, quant à lui, l’aversion d’une population pour l’inégalité et s’exprime en pourcentage (%) : par exemple, un indice d’Atkinson valant 10% signifie que la population est prête à perdre 10% de ses revenus totaux pour avoir une distribution plus égalitaire des revenus. Sa mesure dépend du degré d’aversion de la population pour l’inégalité : plus une population est averse à l’inégalité, plus elle est prête à donner de ses revenus pour une distribution plus égalitaire. noteinegalites14
L’utilisation des rapports interdéciles pour mesurer les inégalités
D’autres indicateurs, reposant sur des rapports au niveau de la distribution des revenus, permettent de mesurer les inégalités de revenus en mettant l’accent sur les revenus des tranches les plus riches et plus pauvres : il s’agit des rapports interdéciles.
3.1 Présentation des rapports interdéciles D9/D1, D5/D1 et D9/D5
Trois principaux rapports interdéciles sont utilisés pour mesurer les inégalités de revenus au sein d’un pays.
Le rapport D9/D1 correspond au ratio entre le niveau de revenus minimum au sein des 10% les plus riches, et le niveau de revenus maximum au sein des 10% les plus pauvres. Il s’agit donc du rapport entre le 9e décile et le 1er décile de la distribution des revenus noteinegalites15 (voir encadré sur la notion de décile).
Le rapport D9/D5 correspond au ratio entre le niveau de revenus minimum au sein des 10% les plus riches et le niveau de revenus médian. noteinegalites16 Dit autrement, il s’obtient en divisant le 9e décile par le 5e décile de la distribution des revenus.
Le rapport D5/D1 correspond au ratio entre le niveau de vie médian et le niveau de vie maximum au sein des 10% les plus pauvres. Il s’obtient donc en divisant le 5e décile par le 1er décile de la distribution des revenus.
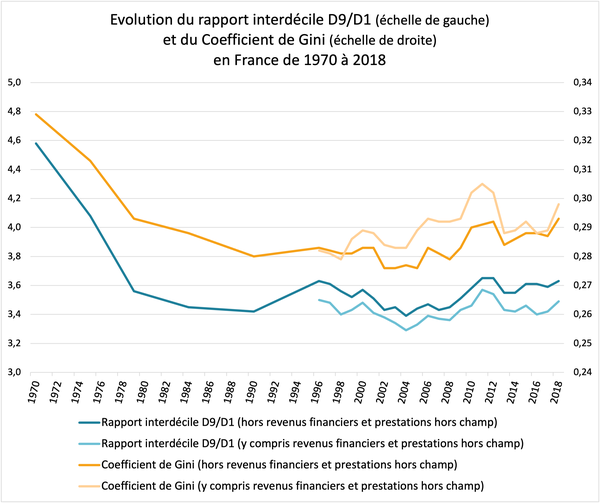
On représente ci-dessous l’évolution du rapport D9/D1 en France pour le niveau de vie. La comparaison avec l’évolution du coefficient de Gini montre que les deux indicateurs proposent la même « histoire » des inégalités de revenus en France.
Source Insee,
Revenus et patrimoine des ménages, édition 2021. Note : l’axe des ordonnées (échelle verticale) de gauche s’applique au rapport interdécile D9/D1 et l’axe des ordonnées de droite s’applique au coefficient de Gini. Le niveau de vie correspond au revenu disponible du ménage rapporté au nombre d’unités de consommation (calculé selon la méthode de l’échelle de l’OCDE modifiée).
Lecture : en 1970, le rapport interdécile D9/D1 en France est de 4,58 (c’est-à-dire que le seuil de revenu au-dessus duquel se situent les 10% de ménages les plus aisés est 4,58 fois plus important que le seuil de revenu au-dessous duquel se situent les 10% de ménages les pauvres). En 1970, le coefficient de Gini en France est de 0,329.
Néanmoins, changer d’indicateur peut parfois mener à des conclusions différentes. Le graphique ci-après représente le rapport interdécile pour les pays de l’Union européenne en 2019.
Rapport interdécile D9/D1 pour les pays de l’Union européenne en 2019
Lecture : en 2019, en Slovaquie, le rapport interdécile D9/D1 est de 2,7 (c’est-à-dire que le seuil de revenu au-dessus duquel se situent les 10% de ménages les plus aisés est 2,7 fois plus important que le seuil de revenu au-dessous duquel se situent les 10% de ménages les plus modestes).
Comme on a pu le voir avec le coefficient de Gini, la Slovaquie est le pays le plus égalitaire et la Bulgarie le pays le plus inégalitaire. Cependant, on remarque aussi qu’en 2019, la France a un coefficient de Gini supérieur à celui de la Croatie, tandis que son rapport interdécile D9/D1 est inférieur. En d’autres termes, la France est moins égalitaire que la Croatie du point de vue du coefficient de Gini, mais plus égalitaire que la Croatie du point de vue du rapport interdécile D9/D1.
Cet exemple fait ressortir l’idée qu’il n’y a pas qu’une seule manière de mesurer les inégalités.
3.2 Critiques des rapports interdéciles
Bien que n’étant pas des indicateurs synthétiques, les rapports interdéciles, et notamment le rapport D9/D1, sont critiqués pour être « aveugles » à ce qui se passe au sein des tranches les plus riches et plus pauvres.
Pour le comprendre, revenons à ce que mesure le rapport D9/D1. C’est le ratio entre le niveau de revenus minimum au sein des 10% les plus riches et le niveau de revenus maximum au sein des 10% les plus pauvres. Par conséquent, tant que ces deux seuils restent inchangés, le ratio D9/D1 reste inchangé. Néanmoins, cela ne donne aucune information sur ce qui se passe au sein-même des 10% les plus riches : typiquement, si le niveau de revenus des 5% les plus riches double alors que le niveau de revenus du reste des ménages stagne, cela ne change en rien le rapport D9/D1. Pourtant, on pourrait raisonnablement vouloir qualifier cette évolution comme correspondant à une augmentation des inégalités. noteinegalites17
Rapports de masses, ratio de Palma et tables de répartition
Pour répondre à la critique faite aux rapports interdéciles, on peut considérer des indicateurs qui prennent en compte non pas des seuils de revenus mais des masses de revenus.
4.1 Le rapport interquintile des masses
Noté (100-S80)/S20 ou S80/S20, le rapport interquintile des masses correspond au ratio entre le revenu total perçu par les 20% les plus riches et le revenu total perçu par les 20% les plus pauvres. Contrairement au rapport interdécile D9/D1, cet indicateur est sensible à ce qui se passe au sein des tranches les plus pauvres et les plus riches. Si on reprend l’exemple du paragraphe précédent – à savoir un doublement des revenus des 5% les plus riches – on aurait une augmentation du rapport interquintile des masses, synonyme d’une augmentation des inégalités.
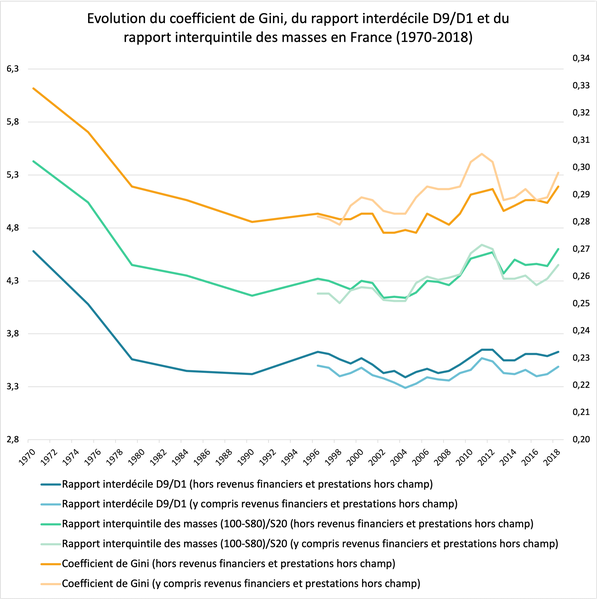
Dans le cas précis de la France, on peut voir ci-dessous que les trois indicateurs – coefficient de Gini, rapport interdécile D9/D1 et rapport interquintile des masses – présentent des évolutions similaires au cours du temps : les inégalités de revenus sont en augmentation globale depuis les années 1980 malgré une légère diminution depuis 2011.
Source Insee,
Revenus et patrimoine des ménages, édition 2021. Note : l’axe des ordonnées de gauche s’applique au rapport interquintile des masses et au rapport interdécile D9/D1 tandis que l’axe des ordonnées de droite s’applique au coefficient de Gini. Le niveau de vie correspond au revenu disponible du ménage rapporté au nombre d’unités de consommation (calculé selon la méthode de l’échelle de l’OCDE modifiée).
Lecture : en 1970, en France, le rapport interquintile des masses en France est de 5,43 (c’est-à-dire que les 20% de ménages les plus aisés perçoivent une masse de revenus 5,43 fois plus importante que l'ensemble des 20% les plus modestes, alors que ces derniers sont quatre fois plus nombreux).En 1970, en France, le rapport interdécile D9/D1 est de 4,58 (c’est-à-dire que le seuil de revenu au-dessus duquel se situent les 10% de ménages les plus aisés est 4,58 fois plus important que le seuil de revenu au-dessous duquel se situent les 10% de ménages les plus modestes). En 1970, en France, le coefficient de Gini est de 0,329.
Des variantes au rapport interquintile des masses sont possibles, dont une particulièrement en vogue : le ratio de Palma. Il se définit comme le ratio entre le revenu total perçu par les 10% les plus riches et celui perçu par les 40% les plus pauvres.
Contrairement au rapport interquintile des masses, le ratio de Palma n’est pas symétrique : on considère seulement les 10% des plus riches contre les 40% les plus pauvres. Pour justifier cela, l’économiste J.G. Palma a introduit l’idée de homogeneous middles versus heterogeneous tails. En comparant différents pays, il a remarqué une hétérogénéité importante dans la part des revenus perçus par les 40% les plus pauvres et les 10% les plus riches tandis que les autres – ceux au « milieu de la distribution », i.e. les homogeneous middles qui rassemblent 50% des ménages – représentent quasi-systématiquement 50% du revenu national. noteinegalites18
La représentation ci-dessous de l’évolution du ratio de Palma en France nous apprend qu’au milieu des années 1990, les 10% les plus riches gagnaient, au total, autant que les 40% les plus pauvres, alors qu’ils étaient quatre fois moins… Aussi, et ce malgré des fluctuations – et un pic en 2011, comme pour le coefficient de Gini par exemple –, le ratio de Palma a eu tendance à augmenter depuis 1996, témoignant d’une augmentation des inégalités en France.
Evolution du ratio de Palma en France (1996-2019)
Lecture : en 1996, le ratio de Palma en France est de 1,01 (c’est-à-dire que les 10% de ménages les plus aisés perçoivent une masse de revenus 1,01 fois plus importante que l'ensemble des 40% les plus modestes, alors que ces derniers sont quatre fois plus nombreux).
Source Insee (repris par l’
Observatoire des Inégalités). Note : le niveau de vie correspond au revenu disponible du ménage rapporté au nombre d’unités de consommation (calculé selon la méthode de l’échelle de l’OCDE modifiée).
4.3 Les tables de répartition et le cas des très hauts revenus
Enfin, une autre approche possible consiste à regarder l’évolution de la part des hauts revenus dans le revenu national. Cette approche, notamment plébiscitée par Thomas Piketty, se prête particulièrement au cas des « ultra-riches ». Concrètement, on représente ci-dessous la part dans le revenu national des revenus perçus par les 1% des ménages ayant les plus hauts revenus en France.
La méthodologie utilisée permet ici d’étudier l’évolution de cet indicateur depuis le début des années 1920 et offre une perspective intéressante. Si on compare les années 1920 aux années 2010, la part dans le revenu national des revenus perçus par les 1% ayant les plus hauts revenus en France a été divisée par deux, passant de 20% à 10%. Cette réduction sur près d’un siècle des inégalités doit cependant être nuancée : en effet, cet indicateur d’inégalités était au plus bas dans les années 1980. Entre 1980 et 2019, les 1% des plus hauts revenus en France ont vu leur part dans le revenu national légèrement augmenter, passant de 8,6% à 10,0% du revenu national en 2019 et témoignant d’un rebond des inégalités de revenus en France.
Une fois de plus, cet exemple illustre l’importance de la fenêtre temporelle d’étude lorsque l’on parle d’inégalités. Avec cet indicateur, la conclusion n’est pas la même si l’on compare les inégalités entre 1920 et 2010 ou si on les compare entre 1980 et 2019…
Part du revenu national perçue par les 1% plus hauts revenus dans le revenu national en France (en %)
Lecture : en 2017, en France, les 1% les plus riches perçoivent 9,8 % de l’ensemble des revenus avant impôts.
Source World Inequality Database. Note : revenus avant impôts et prestations sociales. Le revenu des couples est divisé par deux, sans tenir compte du nombre d'enfants.
Quelques éléments de conclusion
Cette fiche illustre la multitude d’approches et de méthodes possibles pour mesurer les inégalités monétaires. Une première distinction est nécessaire : séparer les inégalités de patrimoine et inégalités de revenus.
L’étude des inégalités de patrimoine permet, entre autres, de souligner l’enrichissement relatif des très grandes fortunes à l’échelle mondiale depuis les années 1980.
Les inégalités de revenus sont généralement mesurées en utilisant le revenu disponible ou le niveau de vie des ménages. Une attention particulière doit être accordée à la fenêtre temporelle d’étude des inégalités. Par exemple, en France, on remarque une réduction des inégalités entre 2011 et 2019. Néanmoins, cela dissimule une tendance plus globale, à savoir que les inégalités aujourd’hui sont légèrement plus marquées qu’elles ne l’étaient dans les années 1980.
Il existe de nombreux indicateurs pour mesurer les inégalités de revenus, parmi lesquels le coefficient de Gini, le rapport interdécile D9/D1 ou encore le ratio de Palma. Selon l’indicateur choisi, les conclusions ne sont pas les mêmes. Par exemple, si l’on se réfère au coefficient de Gini, la France est plus inégalitaire que la Croatie en 2019, tandis qu’elle apparaît comme plus égalitaire que la Croatie si l’on utilise le rapport interdécile D9/D1.
Il n’y a donc pas qu’une seule manière de mesurer les inégalités et si l’on souhaite répondre à la question « les inégalités ont-elles augmenté ou diminué en France ? » ou « les inégalités sont-elles plus élevées en France qu’en Allemagne ? », il faut être conscient que la réponse à ces questions peut être différente selon l’indicateur choisi.
 Pour en savoir plus
Pour en savoir plus

 FICHE
FICHE
 Pour en savoir plus
Pour en savoir plus
 Retour
Retour
